How Many Different Planes Are Implicit in the Notation (123) Family

Clarification of crystal lattice planes

Planes with dissimilar Miller indices in cubic crystals

Miller indices form a notation system in crystallography for lattice planes in crystal (Bravais) lattices.

In particular, a family unit of lattice planes of a given (straight) Bravais lattice is determined by three integers h, k, andℓ, the Miller indices. They are written (hkℓ), and denote the family of (parallel) lattice planes (of the given Bravais lattice) orthogonal to ${\displaystyle \mathbf {g} _{hk\ell }=h\mathbf {b_{1}} +chiliad\mathbf {b_{2}} +\ell \mathbf {b_{3}} }$ , where ${\displaystyle \mathbf {b_{i}} }$ are the footing or primitive translation vectors of the reciprocal lattice for the given Bravais lattice. (Note that the aeroplane is not always orthogonal to the linear combination of direct or original lattice vectors ${\displaystyle h\mathbf {a_{1}} +thou\mathbf {a_{2}} +\ell \mathbf {a_{iii}} }$ because the direct lattice vectors demand not be mutually orthogonal.) This is based on the fact that a reciprocal lattice vector ${\displaystyle \mathbf {m} }$ (the vector indicating a reciprocal lattice point from the reciprocal lattice origin) is the wavevector of a aeroplane wave in the Fourier serial of a spatial function (e.g., electronic density function) which periodicity follows the original Bravais lattice, then wavefronts of the plane wave are coincident with parallel lattice planes of the original lattice. Since a measured scattering vector in X-ray crystallography, ${\displaystyle \mathbf {\Delta k} =\mathbf {g} _{\mathrm {out} }-\mathbf {1000} _{\mathrm {in} }}$ with ${\displaystyle \mathbf {k} _{\mathrm {out} }}$ as the outgoing (scattered from a crystal lattice) Ten-ray wavevector and ${\displaystyle \mathbf {thousand} _{\mathrm {in} }}$ as the incoming (toward the crystal lattice) X-ray wavevector, is equal to a reciprocal lattice vector ${\displaystyle \mathbf {g} }$ equally stated by the Laue equations, the measured scattered X-ray peak at each measured handful vector ${\displaystyle \mathbf {\Delta k} }$ is marked past Miller indices. By convention, negative integers are written with a bar, as in three for −iii. The integers are usually written in lowest terms, i.e. their greatest mutual divisor should be 1. Miller indices are besides used to designate reflections in Ten-ray crystallography. In this instance the integers are not necessarily in lowest terms, and can be thought of as corresponding to planes spaced such that the reflections from adjacent planes would accept a phase divergence of exactly one wavelength (2π), regardless of whether there are atoms on all these planes or not.

There are also several related notations:^[ane]

• the notation {hkℓ} denotes the set of all planes that are equivalent to (hkℓ) by the symmetry of the lattice.

In the context of crystal directions (not planes), the respective notations are:

• [hkℓ], with foursquare instead of round brackets, denotes a direction in the footing of the direct lattice vectors instead of the reciprocal lattice; and
• similarly, the notation <hkℓ> denotes the set of all directions that are equivalent to [hkℓ] by symmetry.

Miller indices were introduced in 1839 by the British mineralogist William Hallowes Miller, although an almost identical arrangement (Weiss parameters) had already been used by German mineralogist Christian Samuel Weiss since 1817.^[2] The method was also historically known every bit the Millerian arrangement, and the indices as Millerian,^[3] although this is at present rare.

The Miller indices are defined with respect to any choice of unit cell and not simply with respect to primitive basis vectors, as is sometimes stated.

Definition [edit]

Examples of determining indices for a plane using intercepts with axes; left (111), right (221)

At that place are two equivalent ways to define the meaning of the Miller indices:^[1] via a indicate in the reciprocal lattice, or as the changed intercepts along the lattice vectors. Both definitions are given beneath. In either case, one needs to choose the 3 lattice vectors a₁ , a₂ , and a_three that define the unit prison cell (note that the conventional unit prison cell may be larger than the primitive cell of the Bravais lattice, as the examples below illustrate). Given these, the three primitive reciprocal lattice vectors are also determined (denoted b₁ , b_two , and b_three ).

Then, given the 3 Miller indices h, grand, ℓ, (hkℓ) denotes planes orthogonal to the reciprocal lattice vector:

${\displaystyle \mathbf {thousand} _{hk\ell }=h\mathbf {b} _{one}+k\mathbf {b} _{ii}+\ell \mathbf {b} _{3}.}$

That is, (hkℓ) only indicates a normal to the planes in the ground of the archaic reciprocal lattice vectors. Considering the coordinates are integers, this normal is itself always a reciprocal lattice vector. The requirement of everyman terms means that it is the shortest reciprocal lattice vector in the given management.

Equivalently, (hkℓ) denotes a airplane that intercepts the three points a₁ /h, a₂ /g, and a₃ /ℓ, or some multiple thereof. That is, the Miller indices are proportional to the inverses of the intercepts of the plane, in the ground of the lattice vectors. If one of the indices is nil, it means that the planes do non intersect that centrality (the intercept is "at infinity").

Considering only (hkℓ) planes intersecting 1 or more lattice points (the lattice planes), the perpendicular distance d betwixt adjacent lattice planes is related to the (shortest) reciprocal lattice vector orthogonal to the planes by the formula: ${\displaystyle d=ii\pi /|\mathbf {m} _{hk\ell }|}$ .^[ane]

The related note [hkℓ] denotes the management:

${\displaystyle h\mathbf {a} _{1}+grand\mathbf {a} _{2}+\ell \mathbf {a} _{three}.}$

That is, it uses the directly lattice basis instead of the reciprocal lattice. Notation that [hkℓ] is non by and large normal to the (hkℓ) planes, except in a cubic lattice every bit described beneath.

Case of cubic structures [edit]

For the special instance of simple cubic crystals, the lattice vectors are orthogonal and of equal length (usually denoted a), as are those of the reciprocal lattice. Thus, in this common case, the Miller indices (hkℓ) and [hkℓ] both simply denote normals/directions in Cartesian coordinates.

For cubic crystals with lattice constant a, the spacing d between adjacent (hkℓ) lattice planes is (from above)

${\displaystyle d_{hk\ell }={\frac {a}{\sqrt {h^{2}+chiliad^{two}+\ell ^{ii}}}}}$ .

Because of the symmetry of cubic crystals, information technology is possible to change the place and sign of the integers and have equivalent directions and planes:

• Indices in angle brackets such as ⟨100⟩ denote a family of directions which are equivalent due to symmetry operations, such as [100], [010], [001] or the negative of whatever of those directions.
• Indices in curly brackets or braces such as {100} denote a family of plane normals which are equivalent due to symmetry operations, much the mode angle brackets denote a family unit of directions.

For face up-centered cubic and body-centered cubic lattices, the primitive lattice vectors are not orthogonal. Notwithstanding, in these cases the Miller indices are conventionally defined relative to the lattice vectors of the cubic supercell and hence are again simply the Cartesian directions.

Case of hexagonal and rhombohedral structures [edit]

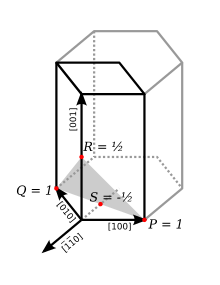
With hexagonal and rhombohedral lattice systems, it is possible to use the Bravais-Miller organisation, which uses four indices (h k i ℓ) that obey the constraint

h + k + i = 0.

Here h, k and ℓ are identical to the corresponding Miller indices, and i is a redundant index.

This four-index scheme for labeling planes in a hexagonal lattice makes permutation symmetries apparent. For instance, the similarity betwixt (110) ≡ (xiii0) and (1two0) ≡ (oneii10) is more obvious when the redundant alphabetize is shown.

In the figure at right, the (001) aeroplane has a three-fold symmetry: it remains unchanged past a rotation of 1/3 (2π/3 rad, 120°). The [100], [010] and the [1 one0] directions are really similar. If South is the intercept of the plane with the [1 ane0] axis, then

i = ane/Southward.

There are also ad hoc schemes (due east.g. in the manual electron microscopy literature) for indexing hexagonal lattice vectors (rather than reciprocal lattice vectors or planes) with four indices. However they don't operate by similarly adding a redundant index to the regular iii-index set.

For example, the reciprocal lattice vector (hkℓ) every bit suggested above can be written in terms of reciprocal lattice vectors as ${\displaystyle h\mathbf {b_{1}} +k\mathbf {b_{2}} +\ell \mathbf {b_{3}} }$ . For hexagonal crystals this may be expressed in terms of direct-lattice basis-vectors a_one , a₂ and a₃ as

${\displaystyle h\mathbf {b_{1}} +thou\mathbf {b_{2}} +\ell \mathbf {b_{three}} ={\frac {2}{3a^{ii}}}(2h+k)\mathbf {a_{1}} +{\frac {two}{3a^{2}}}(h+2k)\mathbf {a_{two}} +{\frac {one}{c^{ii}}}(\ell )\mathbf {a_{3}} .}$

Hence zone indices of the direction perpendicular to aeroplane (hkℓ) are, in suitably normalized triplet form, merely ${\displaystyle [2h+m,h+2k,\ell (3/2)(a/c)^{2}]}$ . When four indices are used for the zone normal to plane (hkℓ), yet, the literature frequently uses ${\displaystyle [h,k,-h-k,\ell (3/two)(a/c)^{two}]}$ instead.^[4] Thus equally you can see, four-index zone indices in square or angle brackets sometimes mix a unmarried directly-lattice index on the correct with reciprocal-lattice indices (normally in circular or curly brackets) on the left.

And, note that for hexagonal interplanar distances, they have the form

${\displaystyle d_{hk\ell }={\frac {a}{\sqrt {{\tfrac {4}{three}}\left(h^{two}+grand^{2}+hk\right)+{\tfrac {a^{2}}{c^{2}}}\ell ^{2}}}}}$

Crystallographic planes and directions [edit]

Dense crystallographic planes

Crystallographic directions are lines linking nodes (atoms, ions or molecules) of a crystal. Similarly, crystallographic planes are planes linking nodes. Some directions and planes have a college density of nodes; these dense planes have an influence on the behavior of the crystal:

• optical properties: in condensed thing, light "jumps" from ane atom to the other with the Rayleigh scattering; the velocity of light thus varies according to the directions, whether the atoms are close or far; this gives the birefringence
• adsorption and reactivity: adsorption and chemical reactions can occur at atoms or molecules on crystal surfaces, these phenomena are thus sensitive to the density of nodes;
• surface tension: the condensation of a material ways that the atoms, ions or molecules are more stable if they are surrounded by other similar species; the surface tension of an interface thus varies according to the density on the surface
  • Pores and crystallites tend to take straight grain boundaries following dense planes
  • cleavage
• dislocations (plastic deformation)
  • the dislocation core tends to spread on dense planes (the elastic perturbation is "diluted"); this reduces the friction (Peierls–Nabarro force), the sliding occurs more frequently on dumbo planes;
  • the perturbation carried by the dislocation (Burgers vector) is along a dense direction: the shift of one node in a dumbo direction is a lesser distortion;
  • the dislocation line tends to follow a dense direction, the dislocation line is often a straight line, a dislocation loop is often a polygon.

For all these reasons, it is important to determine the planes and thus to have a notation arrangement.

Integer vs. irrational Miller indices: Lattice planes and quasicrystals [edit]

Ordinarily, Miller indices are ever integers by definition, and this constraint is physically significant. To understand this, suppose that nosotros allow a plane (abc) where the Miller "indices" a, b and c (defined every bit above) are not necessarily integers.

If a, b and c accept rational ratios, then the same family of planes can exist written in terms of integer indices (hkℓ) by scaling a, b and c appropriately: split by the largest of the iii numbers, and and so multiply by the least common denominator. Thus, integer Miller indices implicitly include indices with all rational ratios. The reason why planes where the components (in the reciprocal-lattice basis) accept rational ratios are of special interest is that these are the lattice planes: they are the only planes whose intersections with the crystal are 2d-periodic.

For a plane (abc) where a, b and c have irrational ratios, on the other hand, the intersection of the plane with the crystal is not periodic. It forms an aperiodic pattern known as a quasicrystal. This structure corresponds precisely to the standard "cut-and-project" method of defining a quasicrystal, using a airplane with irrational-ratio Miller indices. (Although many quasicrystals, such every bit the Penrose tiling, are formed past "cuts" of periodic lattices in more three dimensions, involving the intersection of more than 1 such hyperplane.)

Run across also [edit]

• Crystal structure
• Crystal habit
• Kikuchi line
• Zone axis

References [edit]

1. ^ ^{a b c} Ashcroft, Neil Due west.; Mermin, North. David (1976). Solid state physics . New York: Holt, Rinehart and Winston. ISBN0030839939. OCLC 934604.
2. ^ Weiss, Christian Samuel (1817). "Ueber eine verbesserte Methode für dice Bezeichnung der verschiedenen Flächen eines Krystallisationssystems, nebst Bemerkungen über den Zustand der Polarisierung der Seiten in den Linien der krystallinischen Structur". Abhandlungen der physikalischen Klasse der Königlich-Preussischen Akademie der Wissenschaften: 286–336.
3. ^ Oxford English Dictionary Online (Consulted May 2007)
4. ^ J. W. Edington (1976) Practical electron microscopy in materials science (N. 5. Philips' Gloeilampenfabrieken, Eindhoven) ISBN ane-878907-35-2, Appendix two

External links [edit]

• IUCr Online Dictionary of Crystallography
• Miller index description with diagrams
• Online tutorial well-nigh lattice planes and Miller indices.
• MTEX – Free MATLAB toolbox for Texture Analysis
• http://sourceforge.net/projects/orilib  – A collection of routines for rotation / orientation manipulation, including special tools for crystal orientations.

peytonanympalee.blogspot.com

Source: https://en.wikipedia.org/wiki/Miller_index